The extraordinary life-size terracotta warriors discovered in 1974 near the present day town of Xi'an in China's Shaanxi Province have been excavated and measured (Wenli 1996). The famous statues which were made in the 3 rd century BC, number more than 7000 and are buried in three pits. This amazing terracotta underground army was created in order to symbolically "guard" the mausoleum of the first Chinese Emperor Qin Shi Huangdi. The soldiers are true-to-life (even if the statues are probably not actual portraits), and are buried in battle formation fully armed (Kesner 1995).We analyse here the height of these figures on the basis of a sample of 734 measurements (out of 1087 figures excavated so far), in order to consider the extent to which this imaginary army reflects the actual physical size of the Chinese population of the time (Shaanxi 1988). The mean height of the figures is 177.7 cm (range: 166.0 - 187.5 cm). There was very little difference between the size of the armoured and plain infantry (Table 1).
In considering the distribution of the size of the figures one should consider that the height of human populations is normally distributed; and the standard deviation (σ) of the height distribution of human populations is very close to 6.85 cm even in populations whose meanheight is substantially different. Most military organisations prior to the universal conscription laws of the 19 th century enforced a minimum height requirement (mhr). The measurement of the figures by the archaeologists were made in metric units, which are converted to chi, the linear measure used at the time of the Qin Dynasty (1 chi = 23.0 cm). Their height distribution should be examined in the original measurement units, because that is the appropriate method to identify the mhr for entering the military (Komlos 2002).The measured height ought to be considered an approximation of the true height of the soldiers, insofar as the terracotta figures were assembled from individual components, and therefore, the craftsmen might not have been able to reproduce the true height of the soldiers to the nearest millimetre. In addition, the clay shrank as much as 10 percent in the kiln, and even if the craftsmen probably took this into consideration in production, the final outcome - in most likelihood - might not have reached exactitude to the nearest millimetre (Ledderose 2000). Rather, given these technological considerations, the terracotta statues were probably true-to-life approximations ( 1 ± cm) of contemporary soldiers. Therefore, it should suffice to consider the size distribution of soldiers in increments (bins) of 0.1 chi (2.3 cm); smaller intervals are not warranted (Figure 1). The values indicated are at the centre of the intervals. The size distribution resembles almost precisely the distributions obtained in most military institutions of the 18 th century (Komlos 1989). It indicates that the mhr was probably near 7.65 chi (175.95 cm), because this is the point at which the sample distribution begins to deviate obviously from a normal distribution. The mhr was not enforced stringently, inasmuch as nearly 18 percent of the observations are below the mhr.

Figure 1 (above)
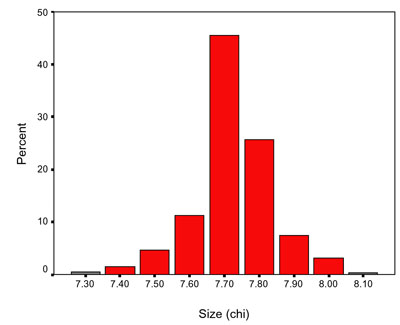
Figure 2
| Type of Figure | N | Size of Figures | S.D. | Min. | Max. | N after Truncation | Truncated Mean |
| Plain infantry | 305 | 177.6 | 2.8 | 168.5 | 187.5 | 236 | 178.7 |
| Armoured infantry | 427 | 177.7 | 2.6 | 166.0 | 186.0 | 365 | 178.4 |
| All | 733 | 177.7 | 2.7 | 166.0 | 187.5 | 601 | 178.5 |

Figure 3
In order to estimate the height of the Chinese population from which the soldiers were drawn, one should calculate the mean of the truncated sample (after the data below the mhr have been discarded), and subsequently, convert these values into population mean estimates by using the above mentioned two attributes of human height distributions, namely that they are normal with a σ = 6.858 cm. We do not use maximum likelihood (ML) method, because the mhr was probably well above the mean, and in such cases ML procedure does not provide the most reliable results (Komlos 1989). Hence, we discard data less than 175.95 cm, because these are not representative of the height of the population from which the soldiers were drawn. The mean sizeof the figures above the mhr is the truncated mean of 178.5 cm (Table 1). This truncated mean translates into a population mean height of 162.3 cm (Table 2). In other words, if one draws a sample from a population with mean of 162.3 cm and σ = 6.858 cm, but limits the sample to those who are taller than 175.95 cm, then the sample obtained will have a mean of 178.5 cm. Admittedly, this estimate is quite sensitive to the assumed values of the mhr and σ. With different plausible values, the estimated height of the Chinese population can range all the way up to 171.2 cm (Table 2). Thus, the mean height of the population cannot be ascertained with certainty, but we can, nonetheless, infer that the size of the terracotta figures could well represent the true physical stature of the Chinese infantry, and these, in turn, could well have been drawn from the population at large. The physical stature of the Chinese population implied by the terracotta figures is certainly within the plausible range, even if one were to subtract 1-2 cm as an allowance for the head-dress and cap of the terracotta figures. The height of Chinese men in the 18th century ranged between 162 and 167 cm (Murray 1994).
The other available body dimensions of the terracotta figures can be compared to those of American soldiers of the Union Army in the 1860s (Table 3) (Gould 1869). Foot length, shoulder width, arm length, as well as the height/arm-length ratio are all remarkably similar, while waistline differs somewhat on account of the different mode of measurement. The head length does differ considerably, but that is caused by the different ethnicity of the Chinese army. All in all, the resemblance of the body dimension to modern populations is quite remarkable.
| Standard Deviation | ||
| mhr | 6.858 | 6.8 |
| Range of Estimates | ||
| min. | max. | |
| 175.95 | 162.3 | 171.1 |
| 175.00 | 166.3 | 171.2 |

Figure 4
| N | cm | s.d. | Source | Comments | |
| Head Length | |||||
| Terracotta US 1860s |
733 10,876 |
24.5 34.3 |
2.7 n/a |
Gould p. 370 | |
| Waistline | |||||
| Terracotta US 1960s |
733 10,876 |
94.6 80.0 |
7.8 n/a |
Gould p.267 | with clothing without clothing |
| Arm Length | |||||
| Terracotta US 1860s |
733 7,889 |
74.5 74.2 |
13.8 n/a |
Gould p.267 | arm + hand length |
| Shoulder Width | |||||
| Terracotta US 1860s |
733 4,085 |
43.5 41.6 |
3.1 n/a |
Gould p.285 | with clothing without clothing |
| Height/Arm Length Ratio | |||||
| Terracotta US 1860s |
733 4,855 |
2.5 2.3 |
0.4 n/a |
Gould p.271 | |
| Foot Length | |||||
| Terracotta US 1860s |
733 6,400 |
27.7 25.6 |
1.6 n/a |
Gould p.271 | with shoes without shoes |
The data for this project were kindly provided by Catharina Blänsdorf of the Bavarian Landesamt für Denkmalpflege, and I take this opportunity to express my appreciation for her support, as well as that of Tianchao Li for help with data processing, without implicating either in the results presented here.
References
- GOULD, Benjamin 1869. Investigations in the Military and Anthropological Statistics of American Soldiers Cambridge: Riverside Press, reprinted Arno Press, NY 1979.
- KESNER, Ladislav, 1995. "Likeness of No One: (Re)presenting the First Emperor's Army," Art Bulletin, 77, 1,: 115-32.
- KOMLOS, John, 1989. Nutrition and Economic Development in the Eighteenth-Century Habsburg Monarchy: An Anthropometric HistoryPrinceton: Princeton University Press.
- KOMLOS, John, 2002. "How To (and How Not to) Analyze Deficient Height Samples," Unpublished Manuscript, University of Munich, 2002; available at: http://www.vwl.uni-muenchen.de/ls_komlos/howto.pdf
- LEDDEROSE, Lothar, 2000. Ten Thousand Things, Module and Mass Production in Chinese Art Princeton: Princeton University Press, pp. 51-74.
- MURRAY, John, 1994."Stature and Body-Mass Index among Mid-Nineteenth Century South Chinese Immigrants, " Annals of Human Biology, 21, 6, 617-620.
- SHAANXI SHENG KAOGU YANJINSUO & SHIHUMAGLING QINYONGKENGKAOGU FAJUEDUI (eds.), Qin Shihuangling bingmayong keng: Yi hao keng fajue baogao, 1974-1984, Beijing: Wenwu Press, 1988, Vol. 1, pp. 349-75.
- WENLI Zhang, 1996. The Qin Terracotta Army. Treasures of Lintong, London: Scala Books.
Komlos, Department of Economics, University of Munich, Ludwigstraße 33/IV, D-80539 Münich, Germany jk@econhist.de